Amplitude Modulation Example #
1. What is Amplitude Modulation? #
Amplitude Modulation (AM) is a method of modulating a carrier wave by varying its amplitude in proportion to the amplitude of the input signal, typically a low-frequency audio signal. The carrier wave’s frequency remains constant, but its amplitude fluctuates according to the instantaneous amplitude of the modulating signal. Figure: Amplitude-modulated wave with a carrier frequency of 500 Hz and a modulation frequency of 100 Hz.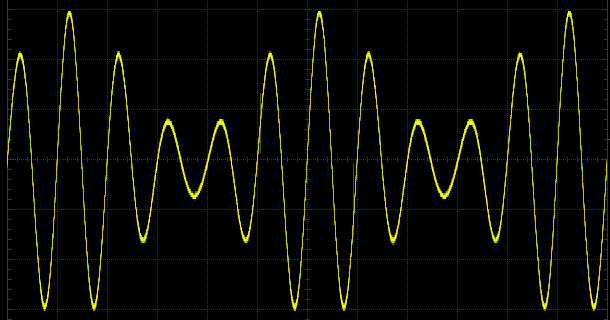
Key Characteristics of AM:
- Carrier Wave: A high-frequency signal used to “carry” the information.
- Modulating Signal: The lower-frequency input signal containing the information to be transmitted.
- Resulting Wave: The modulated wave consists of the carrier frequency and two sidebands (upper and lower), which are mirror images of the modulating signal.
Applications of AM:
- Broadcasting: AM has been widely used in radio broadcasting (e.g., AM radio).
- Communication: Used in aviation and maritime communication due to its simplicity and reliability.
1.1 Multiplicative Form #
The AM wave can be described mathematically using the multiplicative form. If:
- The carrier wave is: $$ c(t) = A_c \sin(2\pi f_c t) $$
- The modulating signal is: $$ m(t) = A_m \sin(2\pi f_m t) $$
Then the AM wave is:
$$ s(t) = \left[A_c + m(t)\right] \sin(2\pi f_c t) $$This equation represents how the amplitude of the carrier wave $ c(t) $ is varied (modulated) by the modulating signal $ m(t) $.
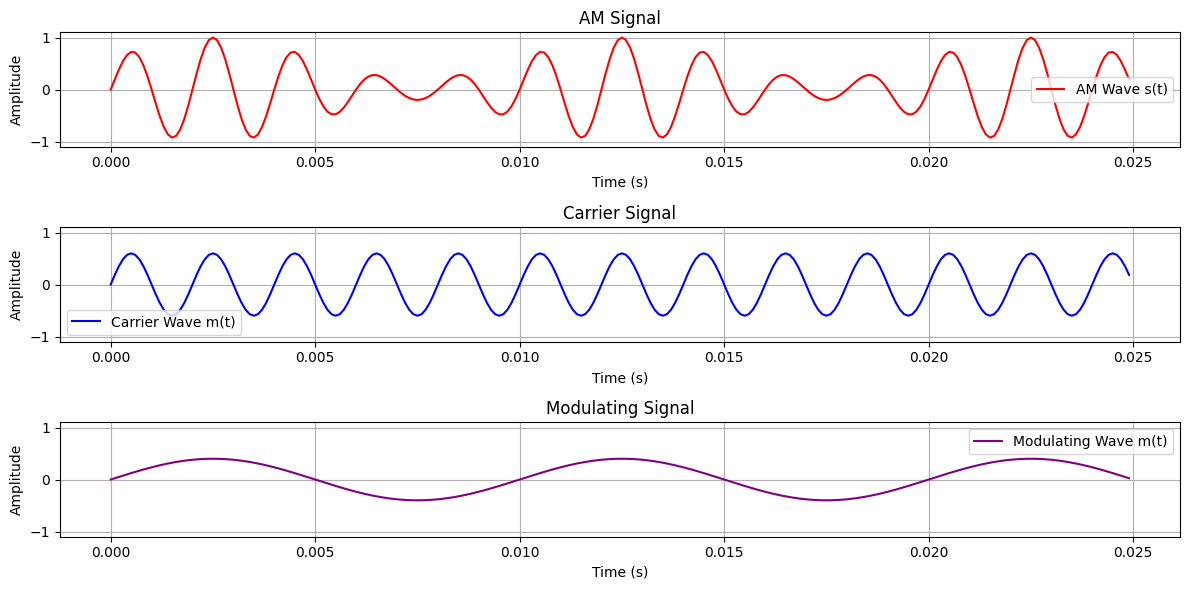
Visualization #
Below is the visualization of:
- $ s(t) $: The resulting AM wave.
- $ c(t) $: The carrier wave.
- $ m(t) $: The modulating signal.
# See code in notebook
1.2 Substitution form #
The AM wave is given by:
$$ s(t) = \left[A_c + m(t)\right] \sin(2\pi f_c t) $$where $ m(t) = A_m \sin(2\pi f_m t) $. Substituting $ m(t) $ into the equation, we get:
$$ s(t) = \left[A_c + A_m \sin(2\pi f_m t)\right] \sin(2\pi f_c t) $$Distribute $ \sin(2\pi f_c t) $:
$$ s(t) = A_c \sin(2\pi f_c t) + A_m \sin(2\pi f_m t) \sin(2\pi f_c t) $$Using the trigonometric identity:
$$ \sin(A) \sin(B) = \frac{1}{2} \left[\cos(A-B) - \cos(A+B)\right] $$we expand $ \sin(2\pi f_m t) \sin(2\pi f_c t) $:
$$ \sin(2\pi f_m t) \sin(2\pi f_c t) = \frac{1}{2} \left[\cos(2\pi (f_c - f_m)t) - \cos(2\pi (f_c + f_m)t)\right] $$Substitute this back into $ s(t) $:
$$ s(t) = A_c \sin(2\pi f_c t) + \frac{A_m}{2} \left[\cos(2\pi (f_c - f_m)t) - \cos(2\pi (f_c + f_m)t)\right] $$Rearranging, we get the final expanded form:
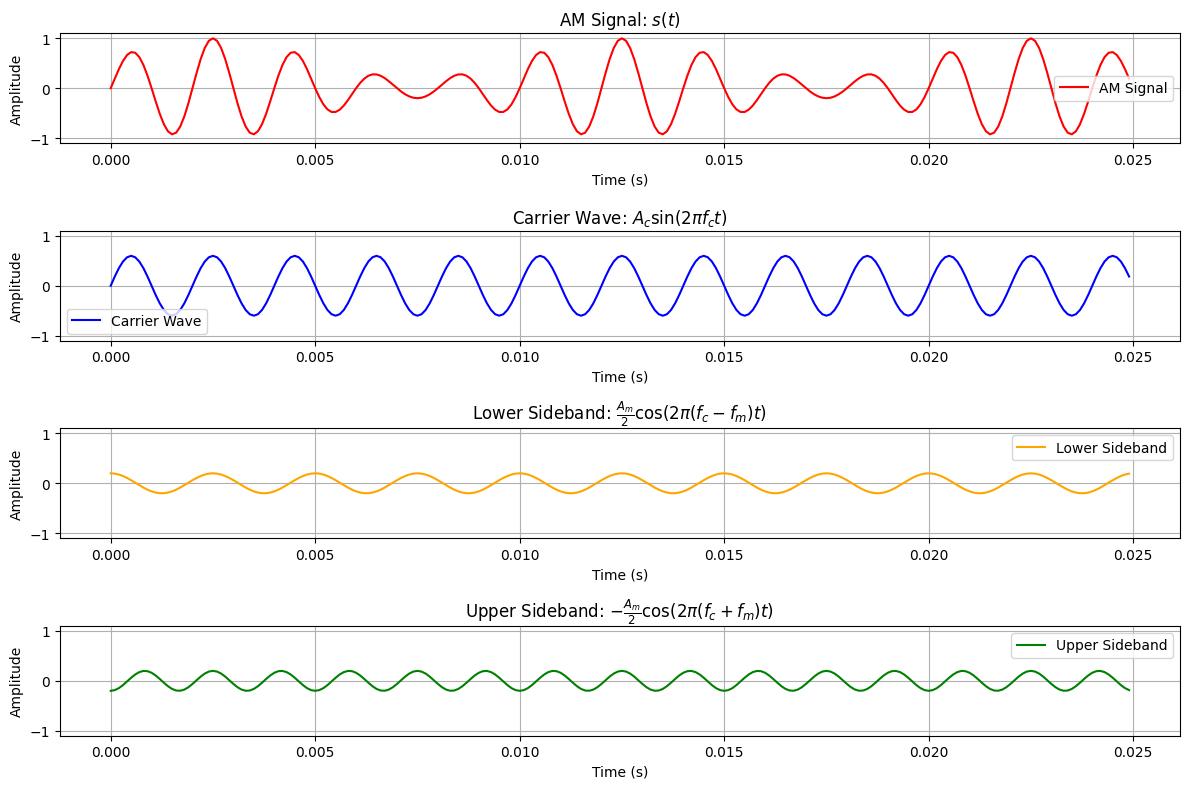
$$ s(t) = A_c \sin(2\pi f_c t) + \frac{A_m}{2} \cos(2\pi (f_c - f_m)t) - \frac{A_m}{2} \cos(2\pi (f_c + f_m)t) $$Visualization #
Below are the plots of:
- The resulting AM Signal: $ s(t) $,
- Carrier Wave: $ A_c \sin(2\pi f_c t) $,
- Lower Sideband: $ \frac{A_m}{2} \cos(2\pi (f_c - f_m)t) $,
- Upper Sideband: $ -\frac{A_m}{2} \cos(2\pi (f_c + f_m)t) $.
# See code in notebook
2. Which Form to Use? #
When generating AM waves, the substitution form is strongly recommended over the multiplicative form due to two key advantages:
2.1 Error Reduction #
The multiplicative form:
$$ s(t) = [A_c + m(t)] \sin(2\pi f_c t) $$requires runtime multiplication of LUT-derived values. This compounds errors from quantization and interpolation, leading to significant inaccuracies in the output.
In contrast, the substitution form:
$$ s(t) = A_c \sin(2\pi f_c t) + \frac{A_m}{2} \cos(2\pi (f_c - f_m)t) - \frac{A_m}{2} \cos(2\pi (f_c + f_m)t) $$avoids runtime multiplication by precomputing the carrier and sideband components. Errors from individual LUTs combine linearly when added, resulting in a much more accurate signal.
2.2 Computational Efficiency #
Addition is inherently faster and less resource-intensive than multiplication, especially on microcontrollers. Using the substitution form:
- Reduces runtime operations to simple additions and LUT lookups.
- Ensures high sampling rates can be achieved without overloading the processor.
- Conserves energy, making it suitable for resource-constrained, battery-powered systems.
2.3 Conclusion #
The substitution form minimizes errors and optimizes performance, making it ideal for real-time AM waveform generation. Its combination of accuracy and computational efficiency ensures reliable operation, even on low-cost microcontrollers.
