Lissajous Curve #

A Lissajous figure is a visual representation of the relationship between two periodic signals plotted against each other in an X-Y coordinate system, with its shape determined by the signals’ frequency ratio, phase difference, and amplitudes.

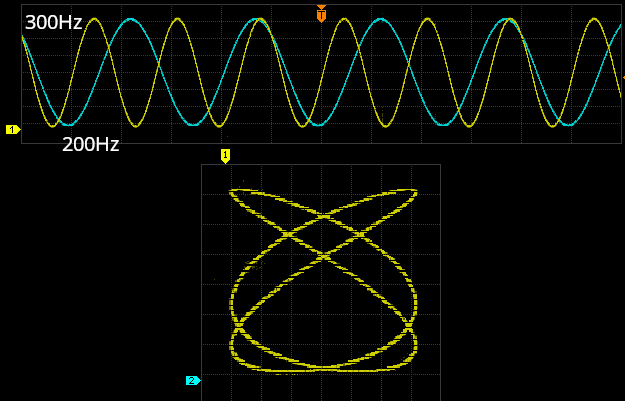
1. The Basics #

• A Lissajous figure is created when two periodic signals are plotted against each other in an X-Y coordinate system: $$ x(t) = A \sin(a t) $$ $$ y(t) = B \sin(b t + \delta) $$ Where:
  • $ A, B $: Amplitudes of the signals.
  • $ a, b $: Angular frequencies of the signals ($ a = 2\pi f_x$ , $ b = 2\pi f_y $).
  • $ \delta $: Phase difference between the signals.

2. Visualizing Phase Differences #

The shape of the Lissajous figure depends heavily on the phase difference ($ \delta $):

• $\delta = 0$: A diagonal line (positive slope) appears when both signals are in phase.
• $\delta = \pi/2$: A perfect circle forms if $ f_x = f_y $ and amplitudes are equal.
• $\delta = \pi$: A diagonal line with a negative slope forms when the signals are 180° out of phase.
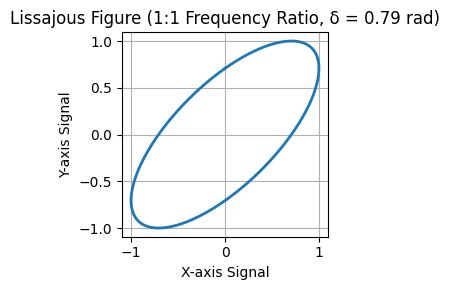
• Intermediate $\delta$: An ellipse forms, with the tilt and eccentricity determined by the phase difference.

Example for Intermediate $\delta$ #

# See code in notebook

3. Visualizing Frequency Ratios #

The frequency ratio ($ f_x : f_y $) determines the complexity of the Lissajous figure:

• 1:1 Ratio ($ f_x = f_y $):
  • The figure is simple and reflects only the phase difference.
  • Examples: Line, circle, or ellipse.
• 2:1 Ratio ($ f_x = 2 f_y $):
  • The figure has two lobes along the X-axis and resembles a “figure-eight.”
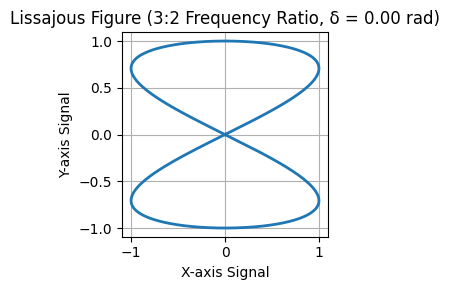
• 3:2 Ratio ($ 2 f_x = 3 f_y $):
  • The figure has three lobes along the X-axis and two lobes along the Y-axis.

For more complex ratios, the pattern becomes more intricate, often requiring careful analysis to interpret.

Example for 3:2 Ratio ($ 2 f_x = 3 f_y $) #

# See code in notebook

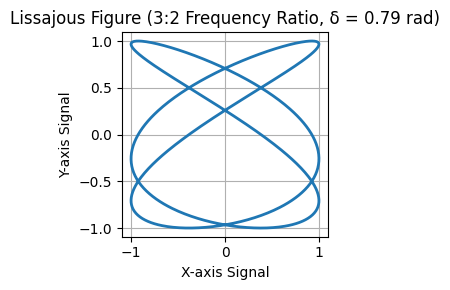
4. Combined Impact of Phase and Frequency #

• Shape of the Figure: The phase difference determines the orientation and symmetry (e.g., diagonal line, tilted ellipse, or circle).
• Complexity of the Figure: The frequency ratio determines the number of lobes or loops in the figure.

Example for Combined Phase and Frequency #

# See code in notebook

5. Practical Steps for Visualization #

1. Generate Two Signals:

   • Use two sinusoidal signals with adjustable frequencies and phase differences.
   • Example:
     • Signal 1: $ x(t) = \sin(2\pi f_x t) $
     • Signal 2: $ y(t) = \sin(2\pi f_y t + \delta) $

2. Set Up an Oscilloscope:

   • Connect Signal 1 to the X-axis and Signal 2 to the Y-axis.
   • Enable X-Y mode on the oscilloscope.

3. Adjust Parameters:

   • Vary $ f_x : f_y $ to explore different patterns.
   • Adjust $ \delta $ to observe how the figure changes.

4. Interpret the Results:

   • Use the figure’s shape to determine the phase difference and frequency ratio.

Summary #

Lissajous figures are influenced by phase difference ($ \delta $) and frequency ratio ($ f_x : f_y $):

• Phase controls the shape (line, circle, ellipse).
• Frequency ratio determines complexity (loops, lobes).