Sweep Wave #
A sweep wave is a waveform where the frequency gradually changes over time instead of remaining constant. This gradual shift in frequency is useful for analyzing system responses, testing circuits, and generating special sound effects.
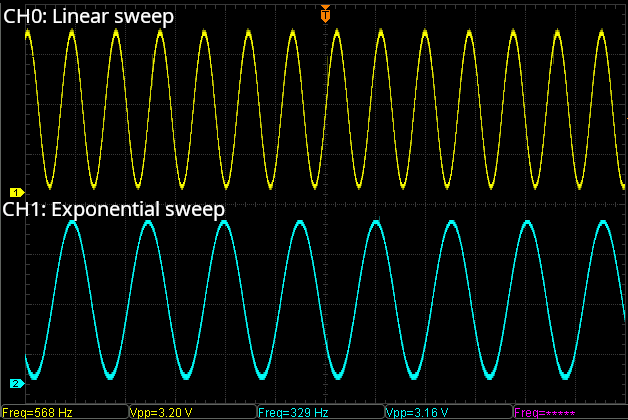
Figure: (a)Frequency at midpoint of the sweep (starting from 100Hz, approaching 1000Hz)
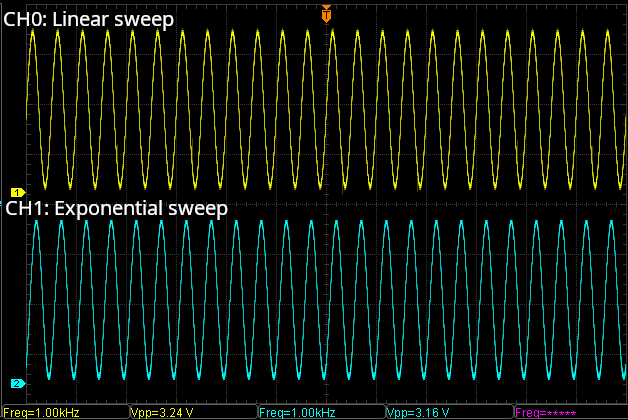
Figure: (b)End of the sweep at 1000Hz
Types of Sweep Waves #
Sweep waves are generally classified into Linear Sweep and Exponential Sweep, each following a distinct mathematical model.
1. Linear Sweep #
A linear sweep increases or decreases frequency at a constant rate over time. The instantaneous frequency $ f(t) $ at time $ t $ is given by:
$$ f(t) = f_{\text{start}} + \frac{(f_{\text{end}} - f_{\text{start}})}{T} \cdot t $$where:
- $ f_{\text{start}} $ is the initial frequency,
- $ f_{\text{end}} $ is the final frequency,
- $ T $ is the total sweep duration,
- $ t $ is the current time.
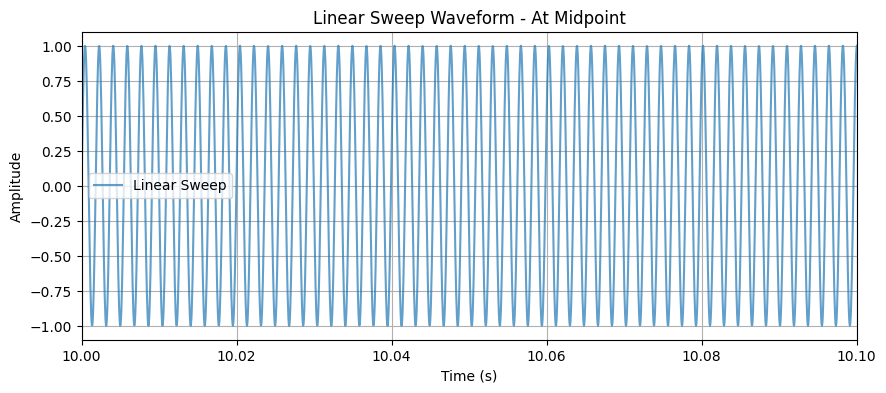
Below is the linear sweep waveform at midpoint of the sweep (starting from 100Hz, approaching 1000Hz):
- The frequency increases linearly, meaning the rate of change remains constant over time.
- The phase is continuously integrated, ensuring smooth waveform transitions.
# See code in notebook
2. Exponential Sweep #
An exponential sweep changes the frequency exponentially, meaning the rate of frequency change is proportional to the frequency itself. The instantaneous frequency is given by:
$$ f(t) = f_{\text{start}} \cdot \left( \frac{f_{\text{end}}}{f_{\text{start}}} \right)^{\frac{t}{T}} $$where:
- $ f_{\text{start}} $ is the initial frequency,
- $ f_{\text{end}} $ is the final frequency,
- $ T $ is the total sweep duration,
- $ t $ is the current time.
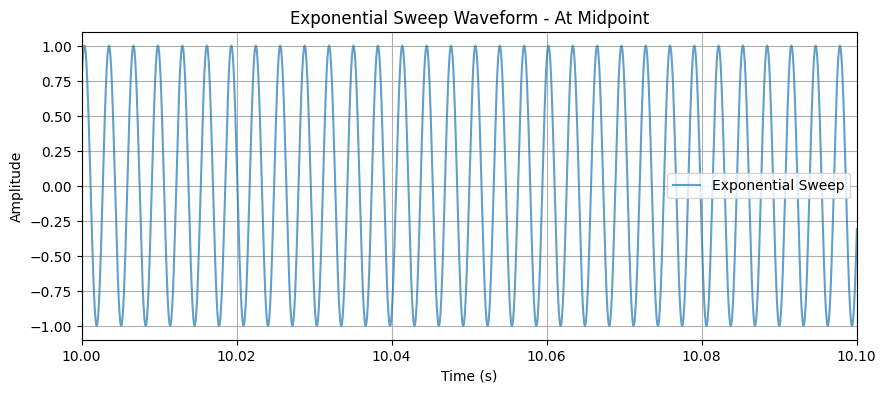
Below is the exponential sweep waveform at midpoint of the sweep (starting from 100Hz, approaching 1000Hz):
- The frequency increases exponentially, producing a smoothly accelerating waveform.
- The phase is continuously integrated, ensuring a completely smooth transition.
# See code in notebook
Choosing Between Linear and Exponential Sweep #
- Linear Sweep: Best for even frequency coverage, suitable for testing audio systems and electronic circuits.
- Exponential Sweep: More natural for hearing perception and used in acoustics and radar applications.
